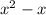Question

If there are x teams in a sports​ league, and all the teams play each other​ twice, a total of​ n(x) games are​ played, where ​n(x)equals

Answer 1

1.
Consider a group of n objects. Assume we want to form groups of r, from these n objects.

There are in total
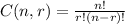
`C(n, r)= (n!)/(r!(n-r)!)` many ways of doing so.

where, r! is "r factorial", calculated as 1*2*3*...*(r-1)*r

2.

C(x, 2) is the total number of pairs out of x objects, that we can form.

so let the x objects represent the x teams, and 2, represent a group of 2, which means a game.

The total number of games is:

n(x)=2*C(x, 2) =
`2* (x!)/(2!(x-2)!)= (x!)/((x-2)!)= (x(x-1)(x-2)!)/((x-2)!)=x(x-1)= x^(2) -x`

Remark, we multiplied by 2, since there will be 2 matches for each pair of teams.


Answer:
`x^(2) -x`