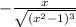Question

Differentiate
1/√x^2-1

Answer 1

the function is
`f(x)= \frac{1}{ \sqrt{ x^(2) -1}}`

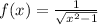
write f again as
`f(x)= (x^(2) -1)^{- (1)/(2) }`

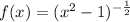
(the power -1 takes the expression to the denominator, and the power 1/2 is square root)

writing rational expressions as power expressions, generally makes differentiation more practical.

In
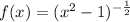
`f(x)= (x^(2) -1)^{- (1)/(2) }` we notice 2 functions:

the outer function
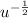
`u^{ -(1)/(2) }`, where
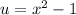
`u=x^(2) -1`, and the inner, u itself , which is a function of x.

So we differentiate by using the chain rule:


`f'(x)= -(1)/(2)u^{- (1)/(2)-1 }*u'= -(1)/(2)u^{- (3)/(2) }*(2x)=- \frac{x}{ \sqrt{ u^(3) } } =- \frac{x}{ \sqrt{ (x^(2) -1)^(3) } }`


Answer:
`- \frac{x}{ \sqrt{ (x^(2) -1)^(3) } }`