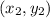Question

It doesn't matter which of the two points on a line you choose to call (x1, y1) and which you choose to call (x2, y2) to calculate the slope of the line.

A. True
B. False

Answer 1

the answer is true

Explanation:

it's what I got

Answer 2

ANSWER

A. True

EXPLANATION

Let


`(x_1,y_1) = (1,2)`



and


`(x_2,y_2) = (2,3)`


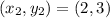
be two points on the straight line.

Then the slope is given by


`m = (y_2-y_1)/(x_2-x_1)`


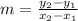
This implies that,


`m = (3 - 2)/(2 - 1) = (1)/(1) = 1`

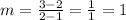
Let us now choose it the other way round,



`(x_1,y_1) = (2,3)`

`(x_2,y_2) = (1,2)`


Then the slope is,


`m = (2 - 3)/(1 - 2) = ( - 1)/( - 1) = 1`

We still had they same result. Hence it doesn't matter which one you choose to call


`(x_1,y_1)`
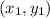
and which to call


`(x_2,y_2)`