Question

I'm in desperate need of help please !!

Answer 1

8a)


`\bf \textit{Amount of Population Growth}\\\\ A=Ie^(rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ I=\textit{initial amount}\\ r=rate\to r\%\to (r)/(100)\\ t=\textit{elapsed time}\\ \end{cases}\qquad \begin{cases} year\ 0\\ -----\\ t=0\\ A=42679 \end{cases} \\\\\\ 42679=Ie^(k0)\implies 42679=I\cdot 1\implies 42679=I\qquad thus \\\\\\ \boxed{A=42679e^(rt)}`

now, let's fast-forward 8 years later, t = 8, the population has dropped to 33247, so A = 33247, what's "r", or in your paper, it uses "k", anyhow, is just the rate.


`\bf A=42679e^(rt)\qquad \begin{cases} t=8\\ A=33247 \end{cases}\implies 33247=42679e^(r8) \\\\\\ \cfrac{33247}{42679}=e^(8r)\impliedby \textit{let's now take \underline{ln} to both sides} \\\\\\ ln\left( (33247)/(42679) \right)=ln(e^(8r))\implies ln\left( (33247)/(42679) \right)=8r\implies \cfrac{ln\left( (33247)/(42679) \right)}{8}=r \\\\\\ -0.0312178\approx r\qquad now\ 100\cdot r\approx -3.1\%`

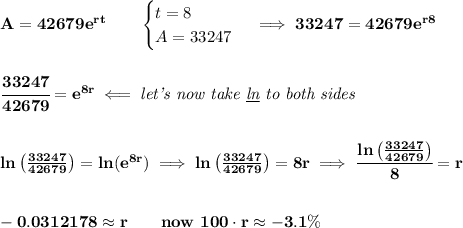
is a negative rate, because, the population is decreasing.

-------------------------------------------------------------------

8)

how many days does it take for 60% of the population to know about the crime? well, what's 60% of 1,150,000? well (60/100) * 1,150,000, or 69000.


`\bf P(t)=1150000e^(-0.03t)\implies 690000=1150000e^(-0.03t) \\\\\\ \cfrac{690000}{1150000}=e^(-0.03t)\implies \cfrac{3}{5}=e^(-0.03t) \\\\\\ \textit{again, we take \underline{ln} to both sides} \\\\\\ ln\left( (3)/(5) \right)=ln(e^(-0.03t))\implies ln\left( (3)/(5) \right)=-0.03t \\\\\\ \cfrac{ln\left( (3)/(5) \right)}{-0.03}=t\implies 17.0275\approx t`

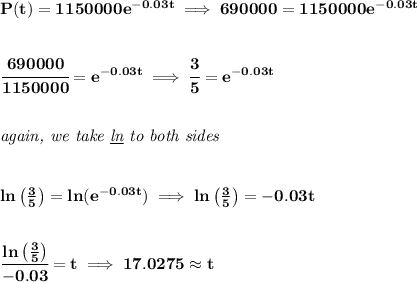
so.. roughly about 17 days.