Answer:
The correct option is c.
Explanation:
The given function is
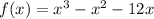
Taking out the common factors.
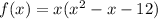
Now, factorize the parenthesis.
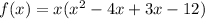
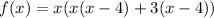
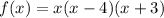
Equate the function equal to 0, to find the zeros of the polynomial function f(x).
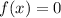

Using zero product property, we get


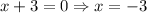
The zeros of the polynomial function f(x) are 0,4,-3. Therefore the correct option is c.