Question

the price of 9-volt batteries is increasing according to the function below, where t is years after January 1, 1980. During what year will the price reach $4? use formula P(t)=1.1*e^0.047t A.)2007 B.)2005 C.)2003 D.)2009

Answer 1

4=1.1e^(0.047t) divide both sides by 1.1

40/11=e^(0.047t) take the natural log of both sides

ln(40/11)=0.047t divide both sides by 0.047

t=ln(40/11)/0.047

t≈24.5

1980+24.5

2007.5

So during 2007 the price will reach $4.

Answer 2

The option A.) 2007 is correct

Explanation:

The formula which is to be used is given :

`P(t) = 1.1\cdot e^(0.047t)`

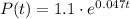
where P(t) is the function of time t and t is the time in years after January 1 , 1980

Now, we need to find the year when the price will reach $4

So, substituting P(t) = 4 and finding the value of t from the given equation.

`\implies 4=1.1\cdot e^(0.047t)\\\\\implies 3.64=e^(0.047t)\\\\\text{Taking natural log ln on both the sides}\\\\\implies \ln 3.64=\ln e^(0.047t)\\\\\implies 1.29=0.047\cdot t\\\\\implies t = 27.49`

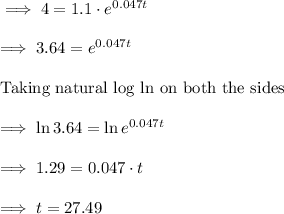
So, t = 27.49 which is approximately equals to 27.5 years

So, 27.5 years after January 1, 1980 is the year 2007

Hence, The price will reach $4 in the year 2007

Therefore, The option A.) 2007 is correct