Question

The cost to produce a product is modeled by the function f(x) = 5x2 − 70x + 258 where x is the number of products produced. Complete the square to determine the minimum cost of producing this product.

Answer 1

5x^2 - 70x + 258

= 5(x^2 - 14x) + 258

= 5[ ( x - 7)^2 - 49) + 258

= 5 (x - 7)^2 - 245 + 258

= 5(x - 7)^2 + 13

Answer 2

The minimum cost of producing this product is:

13

Explanation:

The function which is used to represent the cost to produce x elements is given by:

`f(x)=5x^2-70x+258`

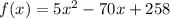
Now, on simplifying this term we have:

`f(x)=5(x^2-14x)+258\\\\i.e.\\\\f(x)=5(x^2+49-49-14x)+258\\\\i.e.\\\\f(x)=5((x-7)^2-49)+258\\\\i.e.\\\\f(x)=5(x-7)^2-5* 49+258\\\\i.e.\\\\f(x)=5(x-7)^2-245+258\\\\i.e.\\\\f(x)=5(x-7)^2+13`

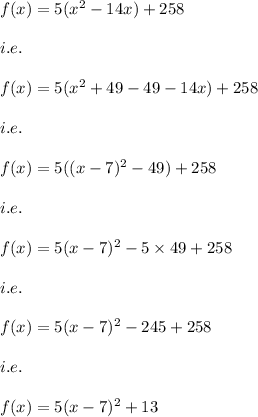
We know that:

`(x-7)^2\geq 0\\\\i.e.\\\\5(x-7)^2\geq 0\\\\i.e.\\\\5(x-7)^2+13\geq 13`

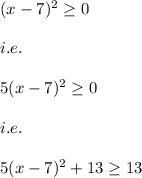
This means that:

`f(x)\geq 13`

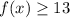
This means that the minimum cost of producing this product is: 13