Question

Marla is looking for a new car. She has test-driven two cars but can only purchase one. The probability that she will purchase car A is 0.52, and the probability that she will purchase car B is 0.38. What is the probability that she will not purchase either car A or car B?

Answer 1

The probability that she won't buy either car is .10. You add the two probabilities that were previously stated and then subtract them from 1.00.

.52 + .38 = .90

1.00 - .90 = .10

Answer 2

Answer: The required probability is 0.10.

Step-by-step explanation: Given that Marla is looking for a new car. She has test-driven two cars A and B but can only purchase one.

We are to find the probability that she will not purchase either car A or car B.

Let, 'C' denotes the event that Marla will purchase car A and 'D' denotes the event that Marla will purchase car 'B'.

Then, according to the given information, we have

`P(A)=0.52,~~~P(B)=0.38.`

Since Marla cannot purchase both the cars, so the events A and B are disjoint.

That is,

`A\cap B=\phi~~~~~\Rightarrow P(A\cap B)=0.`

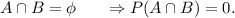
Therefore, the probability that Marla will purchase either car A or car B is given by

`P(A\cup B)=P(A)+P(B)-P(A\cap B)=0.52+0.38-0=0.90.`

Hence, the probability that she will not purchase either car A or car B will be

`P^\prime(A\cup B)=1-P(A\cup B)=0-0.90=0.10.`

Thus, the required probability is 0.10.