Question

(APEX) If a product is equal to zero, we know at least one of the factors must be zero. And the constant factor cannot be zero. So set each binomial factor equal to 0 and solve for x, the width of your project (-2x^-6x-4)

Answer 1

The rule described above is called the Zero Product Property. To illustrate it more clearly, suppose there is a quadratic equation with a general form of ax²+bx+c=0. Because it's degree is 2, then there are two possible roots. When you factor the quadratic equation, that would be

(x-q)(x-r) = 0

where q and r are the roots of the equation. Because their product is zero, the Zero Product Property states that x-q - 0 and x-r = 0

Thus, for the given equation above, a = -2, b = -6 and c=-4. Then, we find the roots using the quadratic formula.


`x= \frac{-b+/- \sqrt{ b^(2)-4ac } }{2a}`

`x= \frac{-(-6)+/- \sqrt{ (-6)^(2)-(-2)(-4) } }{2(-2)}`

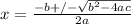
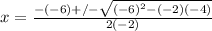
x = -1 and -2. That means q=-1 and r=-2. Hence, the two binomials are (x+1) and (x+2).