Question

A catering service offers 8 appetizers, 11 main courses, and 4 desserts. A banquet chairperson is to select 5 appetizers, 9 main courses, and 2 desserts for a banquet. In how many ways can this be done?

Answer 1

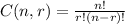
`C(n, r)= (n!)/(r!(n-r)!)` is the formula that calculates the total number of ways that r objects can be selected out of n.

where r!=1*2*3*...*(r-1)*r

for example


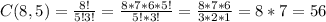
`C(8, 5)= (8!)/(5!3!)= (8*7*6*5!)/(5!*3!)= (8*7*6)/(3*2*1)=8*7=56` is the total number of ways we can pick 5 objects out of 8.

similarly


`C(11, 9)= (11!)/(9!2!)= (11*10*9!)/(9!*2)= (11*10)/(2)=55`


`C(4, 2)= (4!)/(2!2!)= (4*3*2*1)/(2*2)=6`

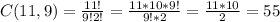
This means that there are 56 ways of picking the appetizers, 55 ways of picking the main courses and 6 ways of picking the desserts.

Since any of the selections of the different meals, can be combined with any selections of the other 2 meals, there are :

56*55*2=6160 ways, of selecting the 3 types of meals.

Answer: 6160