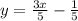
the line does not pass through the point C(5,3)
Step-by-step explanation
Step 1
find the equation of the line, to do that,
a) find the slope using:
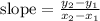
Let
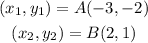
hence, the slope is
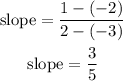
b) using the slope and the point A find the equation
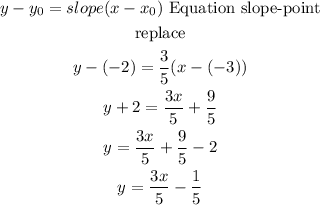
Step 2
Does it also pass through the point C(5,3)?
to answer this you have to replace the values for x and y and check if it is true
Let
C(5,3) x=5 y=3
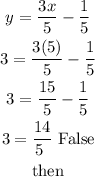
the line does not pass through the point C(5,3)