There are three 'Pythagorean' identities that we can look at and they are
sin²(x) + cos²(x) = 1
tan²(x) + 1 = sec²(x)
1 + cot²(x) = csc²(x)
We can start by checking each option to see which one would give us any of the 'Pythagorean' identities as its simplest form
Option A:
sin²(x) sec²(x) + 1 = tan²(x) csc²(x)
Rewriting sec²(x) as 1/cos²(x)
Rewriting tan²(x) as sin²(x)/cos²(x)
Rewriting csc²(x) as 1/sin²(x)
We have
![sin^(2)(x)[ (1)/( cos^(2)(x) )]+1=[ ( sin^(2)( x))/( cos^(2) (x))][ (1)/( sin^(2)(x) ) ]](https://img.qammunity.org/2018/formulas/mathematics/high-school/k7ll2q13d36bwx1pwp3yojiy6hybwwb2rp.png)
![[( sin^(2)(x) )/( cos^(2)(x) ) ]+1= (1)/( cos^(2)(x) )](https://img.qammunity.org/2018/formulas/mathematics/high-school/ptv48ztelqzn0h6xe6sjd50fpy4jmvo449.png)
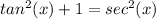
Option B:
sin²(x) - cos²(x) = 1
This expression is already in the simplest form, cannot be simplified further
Option C:
[ csc(x) + cot(x) ]² = 1
Rewriting csc(x) as 1/sin(x)
Rewriting cot(x) as cos(x)/sin(x)
We have
![[ (1)/(sin(x))+ (cos(x))/(sin(x))] ^(2) =1](https://img.qammunity.org/2018/formulas/mathematics/high-school/3efjgj3dmztofwpja30o4kairkvrt50r5a.png)
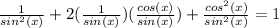
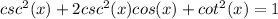
Option D:
csc²(x) + cot²(x) = 1
Rewriting csc²(x) as 1/sin²(x) and cot²(x) as cos²(x)/sin²(x)
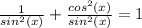
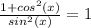
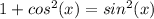

from our working out we can see that option A simplified into one of 'Pythagorean' identities, hence the correct answer