Answer:
Vertex=(-4,3)
Focus=(-4, 2)
Directrix: y=4
Explanation:
Given the equation
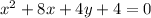
we have to find the vertex, focus, and directrix of parabola.
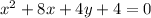
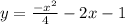

Now, k can be calculated by putting x=4 and y=k in given equation
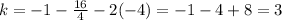
The vertex is (h,k) i.e (-4,3)
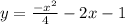
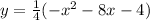
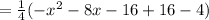
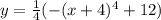
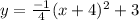
which is required vertex form
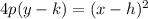
gives p=-1
Focus=(-4, 3+(-1))=(-4,2)
Now directrix can be calculated as
y=3-p=3-(-1)=4