Answer:

Explanation:

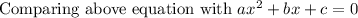
a=3, b=-15, c=20
Discriminant can be calculated as

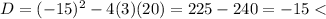
The roots are imaginary
The solution is
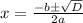
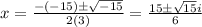
The roots are not real i.e these are imaginary
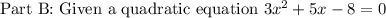
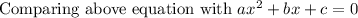
a=3, b=5, c=-8
Discriminant can be calculated as

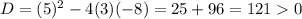
The roots are real
By quadratic formula method
The solution is
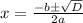
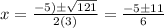
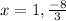
which are required roots.
I choose this method because I can get the solutions directly by substituting the values in formula, and I don't have to guess the possible solutions.