Answer: 304.
Explanation:
The formula to calculate the sample standard deviation is given by :-
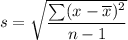
, where x = sample element.
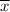 = Sample mean
= Sample mean
s=sample standard deviation.
n= Number of observations.
 = sum of the squared deviations from the sample mean
= sum of the squared deviations from the sample mean
As per given , we have
s=4
n= 20
Substitute theses values in the above formula , we get
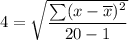
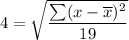
Square root on both sides , we get
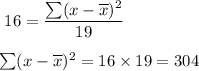
Hence, the sum of the squared deviations from the sample mean is 304.