Question

The perimeter of a triangle is 510 ft and the sides are in the ratio of 11:16:24. Find the area of the triangle. Need help, is there a specific formula for this?

Answer 1

1.
The side lengths are in the ratio 11:16:24, so let them be

11k, 16k, and 24k for some number k.

11k+16k+24k=510
k(11+16+24)=510
51k=510
k=10

so the actual sides are 110, 160 and 240 feet.

2.
There is a famous formula, called Heron's formula, which calculates the area of a triangle, given its sides a, b and c.

we first calculate the half perimeter, which we usually denote by u:


`u= (a+b+c)/(2)`

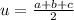
then the theorem states that the area A is as follows:


`A= √(u(u-a)(u-b)(u-c))`

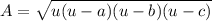
3.

In our case:


`u= (a+b+c)/(2) =(110+160+240)/(2) = (510)/(2)`


`u-a= (510)/(2) -110= (510-220)/(2) = (290)/(2)`


`u-b= (510)/(2) -160= (510-320)/(2) = (190)/(2)`


`u-a= (510)/(2) -240= (510-480)/(2) = (30)/(2)`



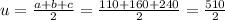
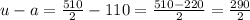
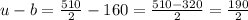
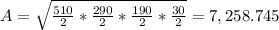`A= \sqrt{(510)/(2)*(290)/(2)* (190)/(2) * (30)/(2)} =7,258.745` feet squared


Answer:D 7,258.745 ft squared