Question

You decide to put $150 in a savings account to save for a $3,000 down payment on a new car. If the account has an interest rate of 2.5% per year and is compounded monthly, how long does it take you to earn $3,000 without depositing any additional funds?

(I know it's 119.954 years, but I have no idea how to get that)

Answer 1

The formula is
A=p (1+r/k)^kt
A future value 3000
P present value 150
R interest rate 0.025
T time?
3000=150 (1+0.025/12)^12t
Solve for t
3000/150=(1+0.025/12)^12t
Take the log
Log (3000/150)=log (1+0.025/12)×12t
12t=Log (3000/150)÷log (1+0.025/12)
T=(log(3,000÷150)÷log(1+0.025÷12))÷12
T=119.95 years

Answer 2

It take 119.954 years to earn $ 3000 without depositing any additional funds.

Explanation:

Given:

Principal Amount, P = $ 150

Amount, A = $ 3000

Rate of interest, R = 2.5% compounded monthly.

To find: Time, T

We use formula of Compound interest formula,

`A=P(1+(R)/(100))^n`

Where, n is no time interest applied.

Since, It is compounded monthly.

R = 2.5/12 %

n = 12T

`3000=150(1+((2.5)/(12))/(100))^(12T)`

`(3000)/(150)=(1+(2.5)/(1200))^(12T)`

`20=(1+(2.5)/(1200))^(12T)`

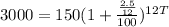
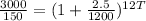
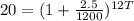
Taking log on both sides, we get

`log\,20=log\,(1+(2.5)/(1200))^(12T)`

`1.30103=12T*\,log\,(1.002083)`

`T=(1.30103)/(12*\,log\,(1.002083))`

`T=119.954`

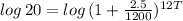
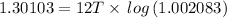
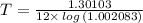
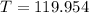
Therefore, It take 119.954 years to earn $ 3000 without depositing any additional funds