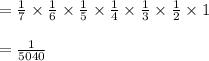Question

You and six friends play a game where each person writes down his or her name on a scrap of paper, and the names are randomly distributed back to each person. Find the probability that everyone gets back his or her own name.

Answer 1

Answer with explanation:

Total number of different candidates who are playing the game=7

Suppose, Seven candidates are represented by ={A,B,C,D,E,F,G}

Total Possible Outcome =7

→Probability that , "A" gets his scrap of paper , means the paper on which he or she has written his or her name

`=\frac{\text{total favorable outcome}}{\text{total favorable outcome}}\\\\=(1)/(7)`

→Now, 6 candidates are left.

Probability that , "B" gets his scrap of paper , means the paper on which he or she has written his or her name

`=\frac{\text{total favorable outcome}}{\text{total favorable outcome}}\\\\=(1)/(6)`

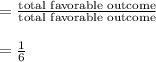
→Now, 5, candidates are left.

Probability that , "C" gets his scrap of paper , means the paper on which he or she has written his or her name

`=\frac{\text{total favorable outcome}}{\text{total favorable outcome}}\\\\=(1)/(5)`

→Now, 4 candidates are left.

Probability that , "D" gets his scrap of paper , means the paper on which he or she has written his or her name

`=\frac{\text{total favorable outcome}}{\text{total favorable outcome}}\\\\=(1)/(4)`

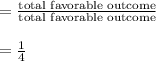
→Now, 3 candidates are left.

Probability that , "E" gets his scrap of paper , means the paper on which he or she has written his or her name

`=\frac{\text{total favorable outcome}}{\text{total favorable outcome}}\\\\=(1)/(3)`

→Now, 2 candidates are left.

Probability that , "F" gets his scrap of paper , means the paper on which he or she has written his or her name

`=\frac{\text{total favorable outcome}}{\text{total favorable outcome}}\\\\=(1)/(2)`

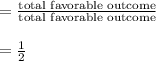
→Now, a single candidates is left.

Probability that , "G" gets his scrap of paper , means the paper on which he or she has written his or her name

`=\frac{\text{total favorable outcome}}{\text{total favorable outcome}}\\\\=(1)/(1)=1`

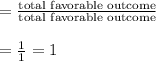
Required Probability

`=(1)/(7) *(1)/(6) *(1)/(5) *(1)/(4) *(1)/(3) *(1)/(2) * 1\\\\=(1)/(5040)`