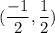Question

What is the general form of the equation for the given circle centered at O(0, 0)? x2 + y2 + 41 = 0 x2 + y2 − 41 = 0 x2 + y2 + x + y − 41 = 0 x2 + y2 + x − y − 41 = 0

Answer 1

I would say the second one.
x^2 + y^2 = 41

Answer 2

The general form of the equation for the given circle centered at O(0, 0) is:

`x^2+y^2-41=0`

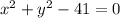
Explanation:

We know that the standard form of circle is given by:

`(x-h)^2+(y-k)^2=r^2`

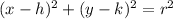
where the circle is centered at (h,k) and the radius of circle is: r units

1)

`x^2+y^2+41=0`

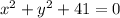
i.e. we have:

`x^2+y^2=-41`

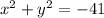
which is not possible.

( Since, the sum of the square of two numbers has to be greater than or equal to 0)

Hence, option: 1 is incorrect.

2)

`x^2+y^2-41=0`

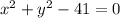
It could also be written as:

`x^2+y^2=41`

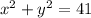
which is also represented by:

`(x-0)^2+(y-0)^2=(√(41))^2`

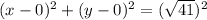
This means that the circle is centered at (0,0).

3)

`x^2+y^2+x+y-41=0`

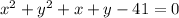
It could be written in standard form by:

`(x+(1)/(2))^2+(y+(1)/(2))^2=(\sqrt{(83)/(2)})^2`

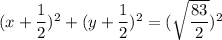
Hence, the circle is centered at
`(-(1)/(2),-(1)/(2))`

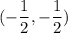
Hence, option: 3 is incorrect.

4)

`x^2+y^2+x-y=41`

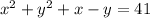
In standard form it could be written by:

`(x+(1)/(2))^2+(y-(1)/(2))^2=(\sqrt{(83)/(2))^2`

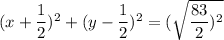
Hence, the circle is centered at:

`((-1)/(2),(1)/(2))`