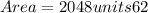Question

Use what you know about special right triangles to find the area of each regular polygon. Leave youranswer in simplest form.I need help with this work question 15

Answer 1

Step-by-step explanation:

Given;

We are given a quadrilateral with a radius of;

`radius=16√(2)`

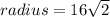
Required;

We are required to find the area of this quadrilateral using ratios of special right triangles.

Step-by-step solution;

We shall begin by making a sketch of the quadrilateral;

Note first of all that a radius is the same length from the center to all sides of a circle. Hence, a quadrilateral with a radius as indicated will have a circle inscribed inside it with the radius touching every part of the circle (and at the same length given). From the diagram sketched above, We can now extract a right angled triangle with two sides measuring 16sqrt2 as indicated. What we would have is an isosceles triangle with one angle measuring 90 degrees and the other two base angles measuring 45 degrees each.

Observe very carefully too that, the radius is also half the length of each side. In other words, each side of the quadrilateral would measure two radii from end to end. This is shown below;

`\begin{gathered} radius=16√(2) \\ length=2* radius \\ Therefore: \\ length=2*16√(2) \\ length=32√(2) \end{gathered}`

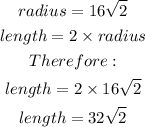
We now have a quadrilateral with the length and width given as;

`\begin{gathered} l=32√(2) \\ w=32√(2) \end{gathered}`

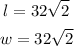
The area of the square would now be;

`\begin{gathered} Area=l* w \\ Therefore: \\ Area=32√(2)*32√(2) \end{gathered}`
`Area=32*32*√(2)*√(2)`
`\begin{gathered} Area=1024*2 \\ Area=2048units^2 \end{gathered}`

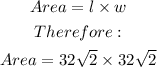
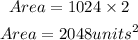
ANSWER:

`Area=2048units62`