ANSWER
475 adult tickets and 375 children tickets were sold
Step-by-step explanation
Let the number of adult tickets be a.
Let the number of children tickets be c.
The total number of tickets is 850. This means that:
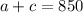
The cost of all the tickets sold is $1512.50.
Each adult's ticket sold for $2.00 and each children ticket sold for $2.00.
Therefore, we have that:
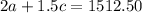
We now have a system of two simultaneous equations:

From the first equation, make a subject of formula:
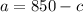
Substitute that into the second equation:
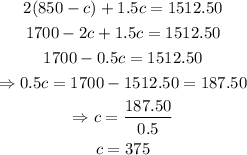
Recall that:
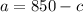
This means that:
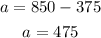
Therefore, 475 adult tickets and 375 children tickets were sold.