Question

An arithmetic sequence is represented in the following table. Enter the missing term of sequence

Answer 1

The required 18th term of the given sequence will be -160

Explanation:

The A.P. is given to be : 44, 28, 12, -4, ....

First term, a = 44

Common Difference, d = 28 - 44

= -12

We need to find the 18th term of the sequence.

`a_n=a+(n-1)* d\\\\\implies a_(18)=44+(18-1)* -12\\\\\implies a_(18)=44+ 17 * -12\\\\\implies a_(18)=44-201\\\\\implies a_(18)=-160`

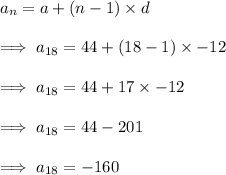
Hence, The required 18th term of the given sequence will be -160

Answer 2

In mathematics, numbered sequential patterns are distinguished as progressions. There are three types of progression: arithmetic, geometric and harmonic. Let's focus on the arithmetic progression.

The pattern in the arithmetic progression is the common difference, You will find that when you subtract two consecutive terms of the sequence, you would get a common difference. Let's investigate further:

28-44 = -16
12-28 = -16
-4-12 = -16

Thus, the common difference is -16. To know the last term, just simply add -16 to the very last known term. In this case, -4+-16 = -20. The answer is -20.