Question

If sin θ = 2 over 7 and tan θ > 0, what is the value of cos θ?

Answer 1

`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad cos(\theta)=\cfrac{adjacent}{hypotenuse} \quad % tangent tan(\theta)=\cfrac{opposite}{adjacent}\\\\ -------------------------------\\\\`


`\bf sin(\theta )=\cfrac{2}{7}\cfrac{\leftarrow opposite}{\leftarrow hypotenuse}\qquad \textit{let's find the adjacent side} \\\\\\ \textit{using the pythagorean theorem}\\\\ c^2=a^2+b^2\implies \pm√(c^2-b^2)=a\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(7^2-2^2)=a\implies \pm√(45)=a\implies \pm 3√(5)=a`

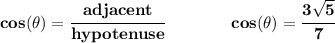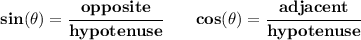
but.... which is it? the + or the -? well, we know that tan(θ) > 0, is another way to say that the tangent of the angle is positive, now, for the tangent to be positive, since it's opposite/adjacent both opposite and adjacent have to be the same exact sign, now, we know the opposite is +2, so that means the adjacent has to be the same sign, thus is the positive version 3√(5)

thus
`\bf cos(\theta)=\cfrac{adjacent}{hypotenuse}\qquad \qquad cos(\theta )=\cfrac{3√(5)}{7}`