Question

10 points! I will thanks, rate, and give best answer!!

Find the 4th term if the sequend in which a 1 = 2 and a n+1 = -4a n + 2

Answer 1

Answer: The fourth term is -102

----------------------------------------------

Step-by-step explanation:

The term after the nth term is generated by this rule
`a_(n+1) = -4(a_n) + 2` which means that we first
Step 1) multiply the nth term (
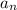
`a_n` ) by -4
Step 2) Add the result of step 1 to the value 2 to get the next term in the sequence

Let's follow those steps above to generate the first four terms

The first term is
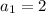
`a_1 = 2`. In short, the first term is 2

The second term is...

`a_(n+1) = -4(a_n) + 2`

`a_(1+1) = -4(a_1) + 2`

`a_(2) = -4(2) + 2`

`a_(2) = -8 + 2`

`a_(2) = -6`
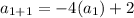
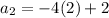
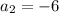
So the second term is -6

The third term is...

`a_(n+1) = -4(a_n) + 2`

`a_(2+1) = -4(a_2) + 2`

`a_(3) = -4(-6) + 2`

`a_(3) = 24 + 2`

`a_(3) = 26`
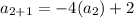
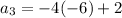
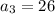
The third term is 26

Finally, the fourth term is...

`a_(n+1) = -4(a_n) + 2`

`a_(3+1) = -4(a_3) + 2`

`a_(4) = -4(26) + 2`

`a_(4) = -104 + 2`

`a_(4) = -102`
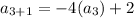
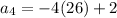
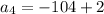
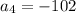The fourth term is -102.