Question

Which is equivalent to 5√1,215^x?

A)243x
B)1,215^1/5x
C)1,215^1/5x
D)243^1/x

Answer 1

Option C is correct

The expression
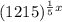`(1215)^{(1)/(5)x}` is equivalent to
`\sqrt[5]{1215^x}`

Explanation:

Simplify the radical Expression:
`\sqrt[5]{1215^x}`

A radical expression can be written by using the exponents and also using the following procedure:

`\sqrt[n]{x} = x^{(1)/(n)}`

when x be non-negative then n can be any index

when x is negative, then n can be odd.

The following radical expression can be written as:

`\sqrt[5]{1215^x} = (1215^x)^{(1)/(5)}` =
`(1215)^{(1)/(5)x}`

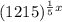
Therefore, the expression
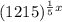`(1215)^{(1)/(5)x}` is equivalent to
`\sqrt[5]{1215^x}`