Question

Bruce had an EKG to measure his heartbeat rate. After conversion, the function produced could be modeled by a cosine function, and the wave produced a maximum of 4, minimum of −2, and period of pi over 2. Which of the following functions could represent Bruce's EKG read-out?

f(x) = 4 cos pi over 2x − 2
f(x) = 3 cos 4x + 1
f(x) = 3 cos pi over 2x + 1
f(x) = 4 cos 4x − 2

Answer 1

y= a.cos (bx) + midline

a = Amplitude = |4+2}/2 = |3|

Period = 2π/b = (2π) / (π/2) = 4

midline = (4-2)/2 = 1

Then the equation is:

y=3.cos(4x) + 1

Answer 2

Option B.

Explanation:

Bruce had an EKG to measure his heartbeat rate. After conversion, the function produced was modeled by a cosine function.

Now we will form this function.

Function will be in the form of f(x) = a cos(Bx) + d

Amplitude
`a=(Maximum-minimum)/(2)`

`a=(4+2)/(2)=3`

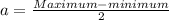
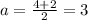
Period = π/2

And
`Period=(2\pi )/(B)`

⇒
`(\pi )/(2)=(2\pi )/(B)`

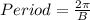
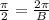
⇒ B = 4

Since minimum is (-2) and maximum is (4), means cosine graph was shifted upwards.

Mid line of the graph is
`x=(4+2)/(2)=3` which shows graph is shifted by one unit above the x-axis.

Now the function we get is f(x) = 3 cos4x + 1

Therefore option B is the answer.