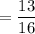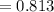Answer:
B. 0.813
Explanation:
A sixteen-sided number cube has the numbers 1 through 16 on each face.
So,
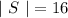
Let us assume that, A be the event that the number will be an even number. So,
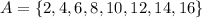 and
and
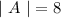
Then,
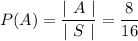
Let us assume that, B be the event that the number will be an odd prime number.
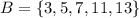 and
and
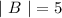
Then,
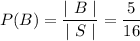
So the probability that you will roll an even number or an odd prime number will be,
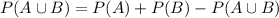
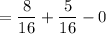 ( as independent events)
( as independent events)