Question

A line passes through (2, –1) and (8, 4).Write an equation for the line in point-slope form.

Rewrite the equation in standard form using integers.

Answer 1

Hello : let A(2,-1) B(8,4)
the slope is : (YB - YA)/(XB -XA)
(4+1)/(8-2) = 5/6

an equation for the line in point-slope form is : y-(-1) =( 5/6)(x-2)
y+1 = (5/6)x -5/3
6y+6 = 5x -10
the equation in standard form is : 5x-6y = 16

Answer 2

Answer: Equation of line in point slope form,

`y + 1 = 5 ( x - 2 )`

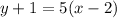
And, Equation of line in standard form,

`5 x - 6 y = 16`

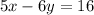
Explanation:

Since, If a line passes through two points
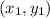`(x_1,y_1)` and
`(x_2,y_2)` ,

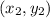Then the equation of line,

`y-y_1=(y_2-y_1)/(x_2-x_1) (x-x_1)`

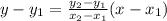
Here
`x_1 = 2`,
`y_1=-1`,
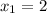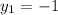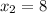`x_2=8` and
`y_2=4`

Thus, the equation of the given line,

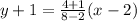
`y-(-1)=(4-(-1))/(8-2) (x-2)`

⇒
`y+1=(4+1)/(8-2) (x-2)`

⇒
`y+1=(5)/(6) (x-2)` -----(1)

⇒
`6(y+1)= 5(x-2)`

⇒ 6 y + 6 = 5 x - 10

⇒ 6 = 5x - 6y - 10 ( By subtracting by on both sides )

⇒ 6 + 10 = 5x - 6y ( By adding 10 on both sides )

⇒ 16 = 5x - 6y

⇒ 5 x - 6 y = 16 ------(2)

Since, in slope for of a line is,
`y-y_1= m (x-x_1)`

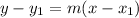
Thus, equation (1) shows the in slope form of the line.

And, standard form of the line is ax + by = c where a, b and c are the integers.

Thus, equation (2) shows the standard form of the given line.