Question

What is the equivalent of pi over 3 radians in degrees?

Answer 1

`\bf \begin{array}{ccllll} radians&d e grees\\ \text{\textemdash\textemdash\textemdash}&\text{\textemdash\textemdash\textemdash}\\ \pi &180\\ (\pi )/(3)&d \end{array}\implies \cfrac{\pi }{(\pi )/(3)}=\cfrac{180}{d}\implies \cfrac{(\pi )/(1)}{(\pi )/(3)}=\cfrac{180}{d} \\\\\\ \cfrac{\pi }{1}\cdot \cfrac{3}{\pi }=\cfrac{180}{d}\implies 3=\cfrac{180}{d}\implies d=\cfrac{180}{3}`

and pretty sure you know how much that is.

Answer 2

Answer: The equivalent expression in degrees is 60°.

Step-by-step explanation: We are given to find the equivalent of the following expression in degrees.

`E=(\pi)/(3)~\textup{radians}.`

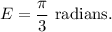
We will be using the UNITARY method the solve the given problem.

We know that

`\pi~\textup{radians}=180^\circ\\\\\\\Rightarrow 1~\textup{radian}=\left((180)/(\pi)\right)^\circ\\\\\\\Rightarrow (\pi)/(3)~\textup{radians}=\left((\pi)/(3)*(180)/(\pi)\right)^\circ=60^\circ.`

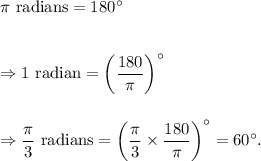
Thus, the equivalent expression in degrees is 60°.