Answer:
The difference between the volumes is 728 ft³.
Explanation:
Our first step will be to find the volume of the smaller pyramid. Notice that we have all the necessary dimensions. The formula for the volume of a pyramid is
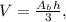
where
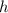 stands for the height and
stands for the height and
 for the area of the basis. In this case
for the area of the basis. In this case
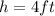 , and the area of the basis, which is a rectangle, is
, and the area of the basis, which is a rectangle, is
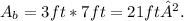 Then,
Then,

Now, two calculate the volume of the second pyramid, recall that it has dimensions three times larger. This means,
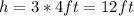 and
and
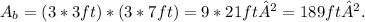 Then,
Then,
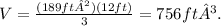
Finally, we only need to substract the values of the volumes:
756 ft³-28 ft³= 728 ft³.