Question

100 POINTS!!!! Create a table of values for a linear function. A drone is in the distance, flying upward in a straight line. It intersects the rainbow at two points. Choose the points where your drone intersects the parabola and create a table for at least four values for the function. Remember to include the two points of intersection in your table. Can you just give me the X and Y values?

Answer 1

So I'm guessing the answer is: any x from -6 to 6; any absolute value > 6 is not meaningful in this case because the x-axis represents the ground level, and no y values can be negative (underground). Range: y values from 0 (ground) up to 36 (an upward measure, in some kind of units). Drone flying upward is y = mx+b; choose m > 0 and b > 0 (e.g. m = 0.5, b = 24)--this will intersect the rainbow twice; you can find those points of intersection by setting the y values of line & parabola =, and solving the resulting quadratic equation by using the quadratic formula. x values of intersection are about -3.60 and 3.35.

Answer 2

Based on the docx you showed me, the equation for the parabola is
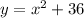
`y = x^2 + 36` and you want a table of values for a linear equation that intersects the parabola at (5, 6) and (-2, 34).

If you use these two points to create a line we get the equation:


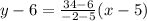
`y - 6 = (34 - 6)/(-2 - 5)(x - 5)` (I just used point slope form)

This can be simplified to:


`y = (40)/(-7)x + (242)/(7)`

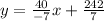
Now we just need to create a table of points on this line. We already have the points you gave and we can also use the y-intercept:
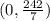
`(0, (242)/(7))` and the x-intercept:
`((121)/(20), 0)`.

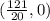
So our table of value can be:

x | y
______|________
-2 | 34
0 | 242 / 7
5 | 6
121/20 | 0