Answer:
The possible range of
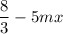 is:
is:
(-9,-3) i.e.

Explanation:
We are given a set of inequalities of the form:
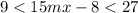
Now when we divide all of the inequality by 3 we get that:

Now when we multiply the inequality by -1 then the sign of the inequality gets interchanged.
i.e.

i.e.

Hence, the possible range of
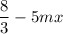 is:
is:
(-9,-3) i.e. between -9 and -3 with -9 and -3 excluded from the range.