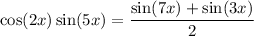Question

Write the product cos(2x)sin(5x) as a sum

Answer 1

The product to sum identity formula states


cos(a)sin(b) = (1/2)[sin(a+b) - sin(a-b)]

So simply plug it into that, to get-

(1/2)[sin(2x+5x) - sin(2x-5x)]

Answer 2

`\cos(2x)\sin(5x)=(\sin (7x)+\sin (3x))/(2)`

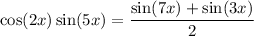
Explanation:

Given:
`\cos(2x)\sin(5x)`

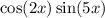
Formula:

`\sin A+\sin B=2\sin((A+B)/(2))\cos((A-B)/(2))`

`\sin((A+B)/(2))\cos((A-B)/(2))=(\sin A+\sin B)/(2)`

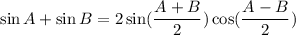
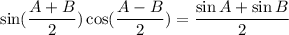
Compare the given expression with formula

`\cos(2x)\sin(5x)=\sin((A+B)/(2))\cos((A-B)/(2))=(\sin A+\sin B)/(2)`

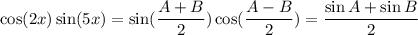
Therefore,

`(A+B)/(2)=5x\Rightarrow A+B=10x`

`(A-B)/(2)=2x\Rightarrow A-B=4x`

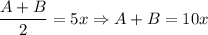
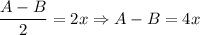
Using two system of equation of A and B to solve for A and B

Add both equation to eliminate B

`2A=14x`

`A=7x`

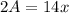
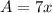
Substitute A into A+B=10x

`7x+B=10x`

`B=3x`

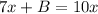
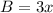
Substitute A and B into formula

`\cos(2x)\sin(5x)=\sin((7x+3x)/(2))\cos((7x-3x)/(2))=(\sin (7x)+\sin (3x))/(2)`

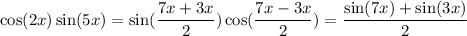
Hence, Product as sum form
`\cos(2x)\sin(5x)=(\sin (7x)+\sin (3x))/(2)`