Question

In a survey of a group of men, the heights in the 20-29 age group were normally distributed, with a mean of 67.1 inches and a standard deviation of 3.0 inches. A studyparticipant is randomly selected. Complete parts (a) through (d) below.(a) Find the probability that a study participant has a height that is less than 68 inches.The probability that the study participant selected at random is less than 68 inches tall is (Round to four decimal places as needed.)(b) Find the probability that a study participant has a height that is between 68 and 72 inches.The probability that the study participant selected at random is between 68 and 72 inches tall is (Round to four decimal places as needed)(c) Find the probability that a study participant has a height that is more than 72 inches.The probability that the study participant selected at random is more than 72 inches tall is (Round to four decimal places as needed.)(d) Identify any unusual events. Explain your reasoning. Choose the correct answer below. A. There are no unusual events because all the probabilities are greater than 0.05. B The events in parts (a), (b), and (c) are unusual because all of their probabilities are less than 0.05. C. The event in part (a) is unusual because its probability is less than 0.05.

Answer 1

The question gives us the mean to be 67.1 and standard deviation to be 3.0.

The heights of the men were normally distributed, hence we can calculate the z score for any age (X) using the formula:

From here, we then proceed to find the probability using the z score from the z distribution table.

This is done below for each subquestion.

Part A:

Probability that height is less than 68.

This is sketched below:

This means that we need the area of the shaded part.

The shaded part contains the entire negative part of the distribution, hence, the total probability of that part must be 0.5.

Now, to get the extra bit slightly greater than the mean 67.1. We do this using the z score formula shown above

`\begin{gathered} z=(X-\mu)/(\sigma) \\ X=68,\mu=67.1,\sigma=3 \\ \therefore z=(68-67.1)/(3) \\ \\ z=0.3 \end{gathered}`

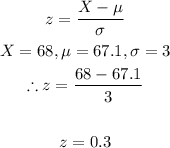
Now, we check z distribution table to find what probability this z value corresponds to.

Answer is: 0.6179

Part B:

If the height is between 68 and 72 inches

we simply find the probability for getting height 72 inches and below and subtract the probability of getting 68 inches and below from our answer.

The cross hatched portion represents the probability of getting between 72 and 68.

The z score for height 72 and below is given below:

`\begin{gathered} z=(72-67.1)/(3) \\ z=1.633 \end{gathered}`

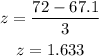
P(z = 1.633) = 0.9484 = Probability of getting 72 and below.

Therefore, the probability of getting between 68 and 72 is:

`0.9484-0.6179=0.3305`

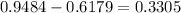
Answer is: P(between 68 and 72) = 0.3305

Part C:

The probability that a participant will get a height above 72 is just the subtraction of the probability of the participant being 72 inches and below in height from 1.

We already got the probability of getting a participant 72 inches and below as :

P(z = 1.633) = 0.9484

`P(\text{above 72 inches)= 1 - 0.9484= 0.0516}`

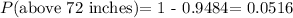
Answer is: 0.0516

Part D:

There are no unusual events because their probabilities are above 0.05 (Option A)