Question

The polar equation r = 7 sin (2theta) graphs as a rose.What is the length of the petals of this rose?Enter your answer in the box.

Answer 1

This problem is about a polar equation. It's important to know that polar coordinates depend on two variables, the angle of the vector and its distance.

`(r,\theta)`

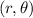
Where r represents the distance and theta represents the angles.

In this case, the angle is 20°, according to the problem.

So, first, we need to graph this equation in the polar system, to then measure the length of the petals

`r=7\sin (2\theta)`

The graph of this equation is shown in the image attached below.

In the image above, you can observe the polar equation graphed, with the coordinated system behind, this will allow us to find the length of each (which are symmetrical). You can observe that the petal on the third quadrant is at (-5,-5).

Now, we use the following formula to find the distance

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

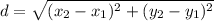
Replacing the points, we have

`d=√((-5)^2+(-5)^2)=√(25+25)=√(2(25))=5√(2)\approx7.07`

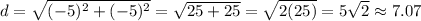
Therefore, the length of each petal is 7.07 units, approximately.