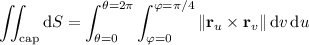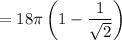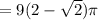Question

Find the surface area of x^2+y^2+z^2=9 that lies above the cone z= sqrt(x^@+y^2)

Answer 1

The cone equation gives


`z=√(x^2+y^2)\implies z^2=x^2+y^2`

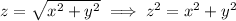
which means that the intersection of the cone and sphere occurs at


`x^2+y^2+(x^2+y^2)=9\implies x^2+y^2=\frac92`

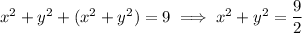
i.e. along the vertical cylinder of radius
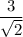
`\frac3{\sqrt2}` when
`z=\frac3{\sqrt2}`.

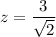
We can parameterize the spherical cap in spherical coordinates by


`\mathbf r(\theta,\varphi)=\langle3\cos\theta\sin\varphi,3\sin\theta\sin\varphi,3\cos\varphi\right\rangle`

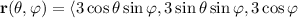
where
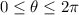
`0\le\theta\le2\pi` and
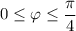
`0\le\varphi\le\frac\pi4`, which follows from the fact that the radius of the sphere is 3 and the height at which the sphere and cone intersect is
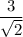
`\frac3{\sqrt2}`. So the angle between the vertical line through the origin and any line through the origin normal to the sphere along the cone's surface is


`\varphi=\cos^(-1)\left(\frac{\frac3{\sqrt2}}3\right)=\cos^(-1)\left(\frac1{\sqrt2}\right)=\frac\pi4`

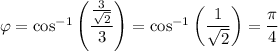
Now the surface area of the cap is given by the surface integral,


`\displaystyle\iint_{\text{cap}}\mathrm dS=\int_(\theta=0)^(\theta=2\pi)\int_(\varphi=0)^(\varphi=\pi/4)\|\mathbf r_u*\mathbf r_v\|\,\mathrm dv\,\mathrm du`

`=\displaystyle\int_(u=0)^(u=2\pi)\int_(\varphi=0)^(\varphi=\pi/4)9\sin v\,\mathrm dv\,\mathrm du`

`=-18\pi\cos v\bigg|_(v=0)^(v=\pi/4)`

`=18\pi\left(1-\frac1{\sqrt2}\right)`

`=9(2-\sqrt2)\pi`