Question

Please help me solve this algebra problem on my homework

Answer 1

We need to determine a few characteristics of the following linear equation:

`y-5=-(1)/(2)(x-2)`

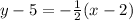
The first step we need to take is to isolate the "y" variable on the left side.

`\begin{gathered} y=(-1)/(2)(x-2)+5 \\ y=(-1)/(2)\cdot x+1+5 \\ y=(-1)/(2)\cdot x+6 \end{gathered}`

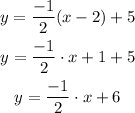
Now we need to analyze this function and provide the necessary characteristics.

First is the Domain. The Domain of a function is the group of all numbers that can be used as an input (x), in this case the Domain is the whole Real group.

Second is the Range, which is the group of numbers that can be the output of the function (y), for this case we also have the whole Real group as Range.

Then we need to find the "Zero". Which is the value at which the function crosses the x-axis, to calculate it we must make "y=0" and solve for x.

`\begin{gathered} 0=(-x)/(2)+6 \\ (x)/(2)=6 \\ x=12 \end{gathered}`

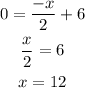
The zero is equal to 12.

The slope of the function is the number multiplying "x", in this case it is -1/2.

The slope is negative, decrescent.

To find the value of f(8), we need to replace x by 8 and solve for y.

`\begin{gathered} f(8)=(-8)/(2)+6 \\ f(8)=-4+6=2 \end{gathered}`

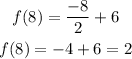
The value of f(8) = 2.

To determine the value of x where f(x) is equal to 5, we need to replace f(x) by 5 and solve for x.

`\begin{gathered} 5=(-x)/(2)+6 \\ (-x)/(2)=5-6 \\ (-x)/(2)=-1 \\ -x=-2 \\ x=2 \end{gathered}`

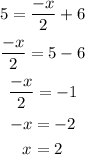
The value of x for which f(x) is equal to 5, is 2.

Now we need to graph the equation, for that we have to use two of the points we found before, we will use (8, 2) and (2,5). We need to mark these points at the coordinate plane and draw a line between them: