Question

Assuming that the equations define x and y implicitly as differentiable functions x=f(t),y=g(t) find the slope of the curve x=f(t), y=g(t) at the given value of t x(t+1)-4tsqrt(x)=9, 2y+4y^3/2=t^3+t , t=0

Answer 1

The given equations are

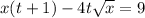
`x(t+1)-4t √(x) =9` (1)

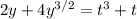
`2y+4y^(3/2)=t^(3)+t` (2)

When t=0, obtain

`x=9 \\ 2y+4y^(3/2)=0 \,\,=\ \textgreater \ \, y(1+2 √(y) )=0 \,=\ \textgreater \ \,y=0`

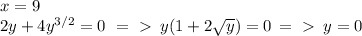
Obtain derivatives of (1) and find x'(0).
x' (t+1) + x - 4√x - 4t*[(1/2)*1/√x = 0
x' (t+1) + x - 4√x -27/√x = 0
When t=0, obtain
x'(0) + x(0) - 4√x(0) = 0
x'(0) + 9 - 4*3 = 0
x'(0) = 3
Here, x' means
`(dx)/(dt)`.

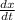
Obtain the derivative of (2) and find y'(0).
2y' + 4*(3/2)*(√y)*(y') = 3t² + 1
When t=0, obtain
2y'(0) +6√y(0) * y'(0) = 1
2y'(0) = 1
y'(0) = 1/2.
Here, y' means
`(dy)/(dt)`.

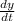
Because
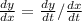
`(dy)/(dx) = (dy)/(dt) / (dx)/(dt)`, obtain

`(dy)/(dx) |_(t=0)\, = (1/2)/(3)= (1)/(6)`

Answer:
The slope of the curve at t=0 is 1/6.