Question

Given that x has a Poisson distribution with

mu
μ
equals
=
13
13​, what is the probability that x
equals
=
5
5​?
​P(
5
5​)
almost equals
≈

0.9930
0.9930 ​(Round to four decimal places as​ needed.)

Answer 1

The Poisson probability distribution function is

`P(x;\mu)= (e^(-\mu)\mu ^(x))/(x!)`
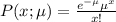
where
μ = mean number of successes
x = actual or expected number of successes

Given:
μ = 13
x = 5

Therefore the probability that x=5 is
P(x = 5) = (e⁻¹³*13⁵)/5!
= 0.8392/120
= 0.006994
= 0.0070 (to 4 dec. places)

Answer: 0.0070 (to 4 decimal places)

It is interesting to observe P(x) as x varies, as in the graph shown below.