Question

A carpenter is assigned the job of expanding a rectangular deck where the width is one-fourth the length. The length of the deck is to be expanded by 6 feet, and the width by 2 feet. If the area of the new rectangular deck is 68 ft2 larger than the area of the original deck, find the dimensions of the original deck.

Answer 1

Let the width be W, then the length is 4W (since the width is 1/4 the length)

The area of the original deck is
`W*4W=4W^(2)`

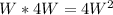
The dimensions of the new deck are :

length = 4W+6
width=W+2

so the area of the new deck is :


`(4W+6)(W+2)= 4W^(2)+8W+6W+12= 4W^(2)+14W+12`

"the area of the new rectangular deck is 68 ft2 larger than the area of the original deck" means that we write the equation:


`4W^(2)+14W+12=68+4W^(2)`


`14W+12=68`


`14W=68-12=56`


`W= (56)/(14)= 4`

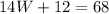
the length is
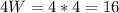`4W=4*4=16` ft


Answer: width: 4, length: 16