Question

A shipment of racquetballs with a mean diameter of 60 mm and a standard deviation of 0.9 mm is normally distributed. By how many standard deviations does a ball bearing with a diameter of 58.2 mm differ from the mean?

Answer 1

Mean 60 - 2(0.9) = 58.2
58.2 is 2 standard deviations from the mean.

Answer 2

By 2 standard deviations a ball does bearing with a diameter of 58.2 mm differ from the mean.

Explanation:

It is given that a shipment of racquetballs with a mean diameter of 60 mm and a standard deviation of 0.9 mm is normally distributed.

`Mean=60`

`\text{Standard deviation}=0.9`

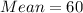
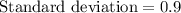
Absolute difference written diameter of 58.2 mm and average diameter is

`|58.2-60|=1.8`

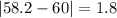
Divide the difference by standard deviation (i.e.,0.9), to find the by how many standard deviations does a ball bearing with a diameter of 58.2 mm differ from the mean.

`(1.8)/(0.9)=2`

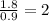
Therefore 2 standard deviations a ball does bearing with a diameter of 58.2 mm differ from the mean.