Question

As a salesperson at Scrapbooks and Treasures, Alysse receives a monthly base pay plus commision on all that she sells. If she sells $400 worth of merchandise in one month, she is paid $388. If she sells $1,000, she is paid $520. Find Alysse's salary when she sells $3,300 worth of merchandise.

Answer 1

In order to find the answer to this, you need to be able to solve for 2 things: what she makes as a base salary and what she makes percentage-wise on her commission. You have information for 2 different equations that will help you here. Set them up as equations, using x and her base salary and y as the percentage of her sales:

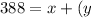
`388=x+(y%*400)` where 388 is what she earns after her base salary, x, is paid and her commission of 400. y is the percent of the commission that she earns. As you can see, we have 2 unknowns, which COULD be a problem. But let's move on first before we freak out.
The next equation involves the other bit of info: that she earns 520 after her base salary of x and her commission of 1000 based on whatever the percentage of her sales is, which is y. That equation looks like this:

`520=x+(y%*1000)`
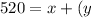
Because her base salary is constant, the x's are the same number in both equations. So we can solve each for x:

`x=-388+400y`

`x=-520+1000y`
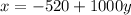
Now that these are both solved for x, and x is the exact same number, we can set those 2 equations equal to each other by the transitive property of equality:
=388+400y= -520+1000y
Solving for y gives you:
132=600y and

`(132)/(600) =y`
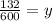
Because this is a percentage, we will multiply the decimal we get by 100 to find that the percentage she earns on a sale is 22%. Now that we have that percentage, we can find her base salary. Do that like this:
Use one of your equations to solve for x:
388=x+[(.22)(400)]
388=x+88 and x = 300. That's her base salary. Now use that base salary in an equation to find out her monthly pay after she sells $3,300 worth of merchandise in a month:
x = 300 + [(.22)(3300)]
x = 300 + 726
x = $1,026
That's how much she makes after her base salary of $300 plus her earning off selling $3,300 worth of merchandise at 22% commission.

Answer 2

Explanation:

In order to solve this we just have to create a system of equations, because we have to unknown values, for the base salary we are going to use X and for the comission we will use Y, now we know that when she sold $400 in merchandise she earned $388 and and when she sold $100 se got paid $520 both equations would look like this:

`x+400y=388\\x+1000y=520]`

Now we can solve them by elimination, multiplying one function by -1.

`(-1)(x+400y=388)= -x-400y=-388\\x+1000y=388\\1000y-400y=132\\600y=388\\y=(132)/(600) \\y=0.22=22%`

Now we know that the percentage that she earns is 22% of the merchandise she sells.

Now to know how much does she makes on her base pay we just put the value into one of the functions:

`x+1000y=520\\x+1000(.22)=520\\x+220=520\\x=300`

So her base pay is $300.

To calculate how much she will earn when she sells $3,300 in merchandise we just put that value into the formula:

`x+3300y=\\300+3300(.22)\\300+726=1026`

So when she sells 3300 she will make 1026 total.