Question

Solve 3x2 + 13x = 10

a. x = two over three and x = −5
b. x = 3 and x = −3
c. x = −2 and x = five over three
d. x = −7 and x = 13

Answer 1

A. x = two over three and x = -5

The equation 3x^2 + 13x = 10 can be solved using the quadratic formula. The solutions are given by:

`$$x = (-b \pm √(b^2 - 4ac))/(2a)$$`

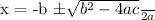
Substituting the values from the equation (where a = 3, b = 13, and c = -10), we get:

`$$x = (-13 \pm √(13^2 - 4*3*(-10)))/(2*3)$$`

This simplifies to:

`$$x = (-13 \pm √(289))/(6)$$`

So, the solutions are:

`$$x = (-13 + √(289))/(6) = (2)/(3)$$`

and

`$$x = (-13 - √(289))/(6) = -5$$`

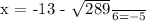
So, the correct answer is A. x = two over three and x = −5.

Answer 2

We want to solve the quadratic equation 3x² + 13x = 10.

Write the equation as
3x² + 13x - 10 = 0

Use the quadratic formula to obtain
x = (1/6) [ -13 +/- √{13² - 4*3*(-10)} ]
= (1/6) [-13 +/- √289]
= (1/6) [-13 +/- 17]
x = -30/6 = -5
or
x = 4/6 = 2/3

The solution is x = 2/3 and -5.

Answer: a