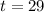Let's find the function p that describes that situation, at the initial time we must pay 400, then
400 - 0
After one month we must pay 290, it will sum with the previous 400 that we have paid
400 - 0
690 - 1 month
In the third month, we must add 400, the previous 290 and 290 again, two times.
400 - 0
690 - 1 month
980 - 2 months
If we repeat that we will see that we will have 290*3 plus 400, in other words, more 290 per month. We can write an expression to do it, it's
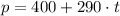
Where t is the time in months, verify that our expression is coherent with our previous logic, now we have our expression let's go to the next step. The lease will be equal to the purchase price when p = 9000, which means that the person paid 9000 on the lease, if we use it in our equation we can solve it for t
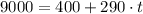
Let's solve it for t
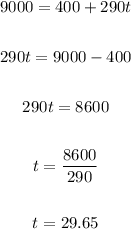
Then, if we lease the motorcycle for 30 months, we will pay $9100, more than the purchase price, if we lease it for 29 months, we will pay $8810.
Final answer:
Expression:
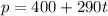
How long you can lease it before it costs more than the purchase price: