Question

Which function is undefined when x= pi/2 radians
cos x
cot x
csc x
tan x

Answer 1

The Cot x is undefined because it is equal to (Sin x)/(Cos x) and at pi/2, Cosine = 0.

Answer 2

Option 4 that is tan x will be undefined at x=pi/2 radians

Explanation:

`(\pi)/(2)radians=90^(\circ)`

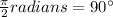
In case 1:

We have cos x

`\text{Cos x has value 0 at x}=(\pi)/(2)radians`

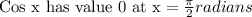
Therefore the function is defined hence, option 1 is discarded.

In case 2:

We have cot x and

`cot x=(cos x)/(sin x)`

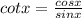
Since,
`\text{cos x at x}=(\pi)/(2)\text{radians is 0}`

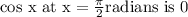
And
`\text{sin x at x}=(\pi)/(2)\text{radians is 1}`

Hence,
`cot x=(0)/(1)=0`

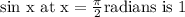
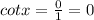
Hence, defined and Option 2 is discarded.

In case 3:

We have csc x and

`csc x=(1)/(sin x)`

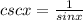
Since,
`\text{sin x at x}=(\pi)/(2)\text{radians is 1}`

Hence,
`csc x=(1)/(1)=1`

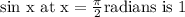
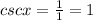
Hence, defined and Option 3 is discarded.

In case 4:

We have tan x and

`tan x=(sin x)/(cos x)`

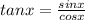
Since,
`\text{cos x at x}=(\pi)/(2)\text{radians is 0}`

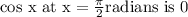
And
`\text{sin x at x}=(\pi)/(2)\text{radians is 1}`

Hence,
`tan x=(1)/(0)=\infty`

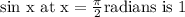
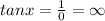
Hence, undefined and Option 4 is correct.