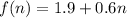Question

This sequence represents the diameters of circles used to create an art project: 2.5 cm, 3.1 cm, 3.7 cm, 4.3 cm Let f(n) represent diameter in centimeters and n the term number in the sequence. Which equation represents the sequence of diameters?

Answer 1

ANSWER

The expression that represent the sequence of diameters is,

`f(n) = 0.6n + 1.9`


EXPLANATION

The terms in the sequence are,


`2.5,3.1,3.7,4.3`


The first term is

`a = 2.5`

The common difference is


`d = 3.1 - 2.5 = 0.6`


The formula for the nth term is given by,



`f(n) = a + (n - 1)d`



We substitute the values in to the formula to get,




`f(n) = 2.5+ (n - 1)0.6`



We expand the parenthesis to obtain,


`f(n) = 2.5 + 0.6n - 0.6`



We rearrange to obtain,


`f(n) = 0.6n + 2.5- 0.6`


We simplify to get,


`f(n) = 0.6n + 1.9`

Answer 2

`f(n) = 1.9 +0.6n`

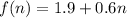
Explanation:

The nth term of the arithmetic sequence is given by:

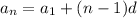`a_n = a_1+(n-1)d` ....[1]

where

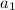`a_1` is the first term

d is the common difference and n is the number of terms.

Here, f(n) represent diameter in centimeters and n the term number in the sequence.

Given the sequence represents the diameters of circles used to create an art project:

2.5 cm, 3.1 cm, 3.7 cm , 4.3 cm

This sequence is an arithmetic sequence with

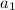`a_1` = 2.5 and d = 0.6

Since,

3.1-2.5 = 0.6,

3.7-3.1 = 0.6

4.3-3.7 = 0.6

Substitute the given values in [1] we have;

`f(n) =2.5+(n-1)(0.6)`

Using distributive property,
`a\cdot (b+c) = a \cdot b+ a\cdot c`we have;

`f(n) = 2.5+0.6n-0.6`

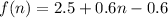
Simplify:

`f(n) = 1.9 +0.6n`

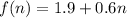
Therefore, the equation represents the sequence of diameters is,
`f(n) = 1.9 +0.6n`