Question

Enter the polynomial function f(x)​ in standard form given that f has leading coefficient 2​ and roots 2​, sqrt{3}​​, and -sqrt{3}​.​​​

Answer 1

Given that a polynomial function
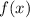`f(x)` has,

• leading coefficient= 2
• roots = 2 , √3 , -√3

And we need to find
`f(x)`

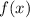
as we know that if a polynomial has zeroes as
`\alpha` ,
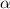`\beta` and
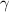`\gamma` , then the cubic polynomial is given by,

`\longrightarrow f(x)=k (x-\alpha)(x-\beta)(x-\gamma)\\`

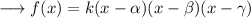
where ,

• k is the leading coefficient.

Now substitute the given zeroes, as ;

`\longrightarrow f(x)=2[ (x-2)(x-\sqrt3)(x+\sqrt3)]\\`

`\longrightarrow f(x)= 2[(x-2)\{ x^2-(\sqrt3)^2\}]`

`\\\longrightarrow f(x)= 2[ (x-2)(x^2-3)]\\`

`\longrightarrow f(x)=2[ x(x^2-3)-2(x^2-3)]\\`

`\longrightarrow f(x)= 2[ x^3-3x -2x^2+6]\\`

`\longrightarrow \underline{\underline{ f(x)= 2x^3-4x^2-6x+12}}`

and we are done!

Answer 2

`f(x)=2x^3-4x^2-6x+12`

Explanation:

Given characteristics of the polynomial:

• leading coefficient = 2​
• roots = 2​, √3, and -√3.​​​

As the polynomial has 3 roots, it is a cubic polynomial.

`\boxed{\begin{minipage}{6 cm}\underline{Intercept form of a cubic polynomial}\\\\$y=a(x-r_1)(x-r_2)(x-r_3)$\\\\where:\\ \phantom{ww}$\bullet$ $r_n$ are the roots. \\ \phantom{ww}$\bullet$ $a$ is the leading constant.\\\end{minipage}}`

Substitute the given leading coefficient and roots into the formula:

`f(x)=2(x-2)(x-√(3))(x+√(3))`

Expand to standard form:

`\implies f(x)=2(x-2)(x+√(3)x-√(3)x-3)`

`\implies f(x)=(2x-4)(x^2-3)`

`\implies f(x)=2x^3-6x-4x^2+12`

`\implies f(x)=2x^3-4x^2-6x+12`