Question

What is the simplified form of 3 over 4x plus 3 + 21 over 8 x squared minus 14x minus 15

6 times the quantity 2 x plus 5 end quantity over the quantity 2x minus 5 end quantity times 4 x plus 3
6 over the quantity 4 x plus 3
6 times the quantity x plus 1 end quantity over the quantity 2x minus 5 end quantity times 4 x plus 3
6 times the quantity x plus 1 end quantity over the quantity 2x plus 5 end quantity times 4 x plus 3

Answer 1

Answer: Third Option is correct.

Step-by-step explanation:

Since we have given that

`(3)/(4x+3)+(21)/(8x^2-14x-15)`

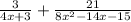
Now, we will simplify it, step by step:

First we take 3 as common factor :

`3[(1)/(4x+3)+(7)/(8x^2-14x-15)]`

Now, we will do the method " Splitting the middle term" we get,

`3[(1)/(4x+3)+(7)/(8x^2-20x+6x-15)]\\\\3[(1)/(4x+3)+(7)/(4x(2x-5)+3(2x-5))]\\\\3[(1)/(4x+3)+(7)/((4x+3)(2x-5))]\\\\3[(2x-5+7)/((2x-5)(4x+3))]\\\\=3[(2x+2)/((2x-5)(4x+3))]\\\\=(6(x+1))/((2x-5)(4x+3))`

Hence, 6 times the quantity x plus 1 end quantity over the quantity 2x minus 5 end quantity times 4x plus 3.

Therefore, Third Option is correct.

Answer 2

First we have to factorize:
8 x² - 14 x - 15 = 8 x² - 20 x + 6 x - 15 =
= 4 x ( 2 x - 5 ) + 3 ( 2 x - 5 ) =
= ( 2 x - 5 ) ( 4 x + 3 )
Then we will put it into the equation:
3 / ( 4 x + 3 ) + 21 / ( 2 x - 5 ) ( 4 x + 3 ) =
= 3 ( 2 x - 5 ) + 21 / ( 2 x - 5 ) ( 4 x + 3 ) =
= 6 x - 15 + 21 / ( 2 x - 5 ) ( 4 x + 3 ) =
= (6 x + 6) / ( 2 x - 5 ) ( 4 x + 3 ) =
= 6 ( x + 1 ) / ( 2 x - 5 ) ( 4 x + 3 )
Answer: C ) 6 times the quantity x plus 1 end over the quantity 2 x minus 5 end quantity times 4 x plus 3.