Question

The table below shows four systems of equations: System 1 System 2 System 3 System 4 4x − 5y = 2 3x − y = 8 4x − 5y = 2 10x − 7y = 18 4x − 5y = 2 3x − 8y = 4 4x − 5y = 2 10x + 3y = 15 Which pair of systems will have the same solution?

Answer 1

The system b is the same

Answer 2

System 1 and System 2 are equivalent.

Explanation:

The first and second system have the same solutions, the are equivalent systems of equations. Let's calculate solutions to demonstrate it:

System 1.

`\left \{ {{4x - 5y = 2} \atop { 3x - y = 8}} \right.`

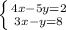
If we multiply the second equations by -5, we can eliminate one variable and find the first solution:

`\left \{ {{4x - 5y = 2} \atop { -15x +5y = -40}} \right.\\-11x=-38\\x=(38)/(11)`

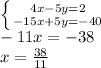
Now, we use this value to find the other solution:

`3x - y = 8\\3((38)/(11))-y=8\\(114)/(11)-8=y\\ y=(114-88)/(11)=(26)/(11)`

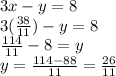
The solution of the first system is
`((38)/(11) ;(26)/(11) )`

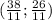
System 2.

`\left \{ {{4x - 5y = 2} \atop { 10x - 7y = 18}} \right.`

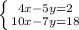
We do the same process than we did before, but this time we have to multiply by
`-(5)/(7)`:

`\left \{ {{4x - 5y = 2} \atop { -(50)/(7)x + 5y = (90)/(7) }} \right.\\(28x-50x)/(7)=(-90+14)/(7)\\-22x=-76\\x=(38)/(11)`

Then,

`4x - 5y = 2\\4((38)/(11))-5y=2\\(152)/(11)-2=5y\\ 5y=(152-22)/(11)\\y=(130)/(5(11))=(26)/(11)`

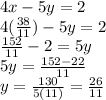
The solution of the second system is
`((38)/(11) ;(26)/(11) )`

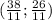
Therefore, system 1 and system 2 are equivalent.