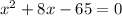Question

A square picture with a side length of 4 inches needs to be enlarged. The final area needs to be 81 square inches.

Which equation can be used to solve for x, the increase in side length of the square in inches?

x2 + 4x – 81 = 0
x2 + 4x – 65 = 0
x2 + 8x – 65 = 0
x2 + 8x – 81 = 0

Answer 1

`x^2+8x-65=0`

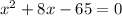
Explanation:

Side length of square = 4 inches

Let x be the increase in length

So, New length = x+4

Area of square =
`Side^2`

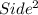
Area of enlarged square =
`(x+4)^2`

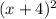
Using identity :
`(a+b)^2=a^2+b^2+2ab`

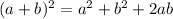
Area of enlarged square =
`x^2+16+8x`

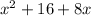
We are given that The final area needs to be 81 square inches.

So,
`x^2+16+8x=81`

`x^2+16+8x-81=0`

`x^2+8x-65=0`

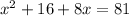
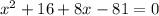
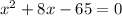
So, Option C is true

Hence equation can be used to solve for x, the increase in side length of the square in inches is
`x^2+8x-65=0`

Answer 2

Let x be the "enlargement value" of each side :
Then the enlarged side becomes (x+4) and the square = (x+4)²
The final area should be (x+4)² = 81
Let's expand:
x²+ 8x + 16 = 81
x² + 8x + 16 - 81 = 0
x² + 8x - 65 = 0